XOR DSL ​

XOR DSL is a privacy-preserving composition library supporting local computations on private datasets, secure multi-party computations (MPC) as well as federated learning (FL) computations with secure aggregation. It is extensible to other cryptographic techniques such as differential privacy (DP) and fully-homomorphic encryption (FHE). It enables developing complex programs using an elegant, domain-specific language (DSL).

Goals ​

XOR DSL is a Scala library that makes it easier to write privacy-preserving programs. In particular, XOR DSL

• allows the use of modern-day programming features to better abstract and compose code (e.g. classes, functions, algebraic data types)
• provides data structures to represent certain privacy-preserving graphs and a user-friendly API to construct such graphs
• makes it easier to plug in custom static analysis tools and optimizers for privacy-preserving code (e.g. statistical and probabilistic code analysis tools such as masking distribution calculators (for MPC), noise parameters calculators (for FHE and DP))
• makes it possible to execute a program on different privacy-preserving backends
• enables intuitive composition of different privacy-preserving programs including
  local computations on private data via custom scripts and existing libraries such as PyTorch and Tensorflow among others
• interacts with the XOR Secret Computing platform and executes your privacy-preserving application

Foundations of XOR DSL ​

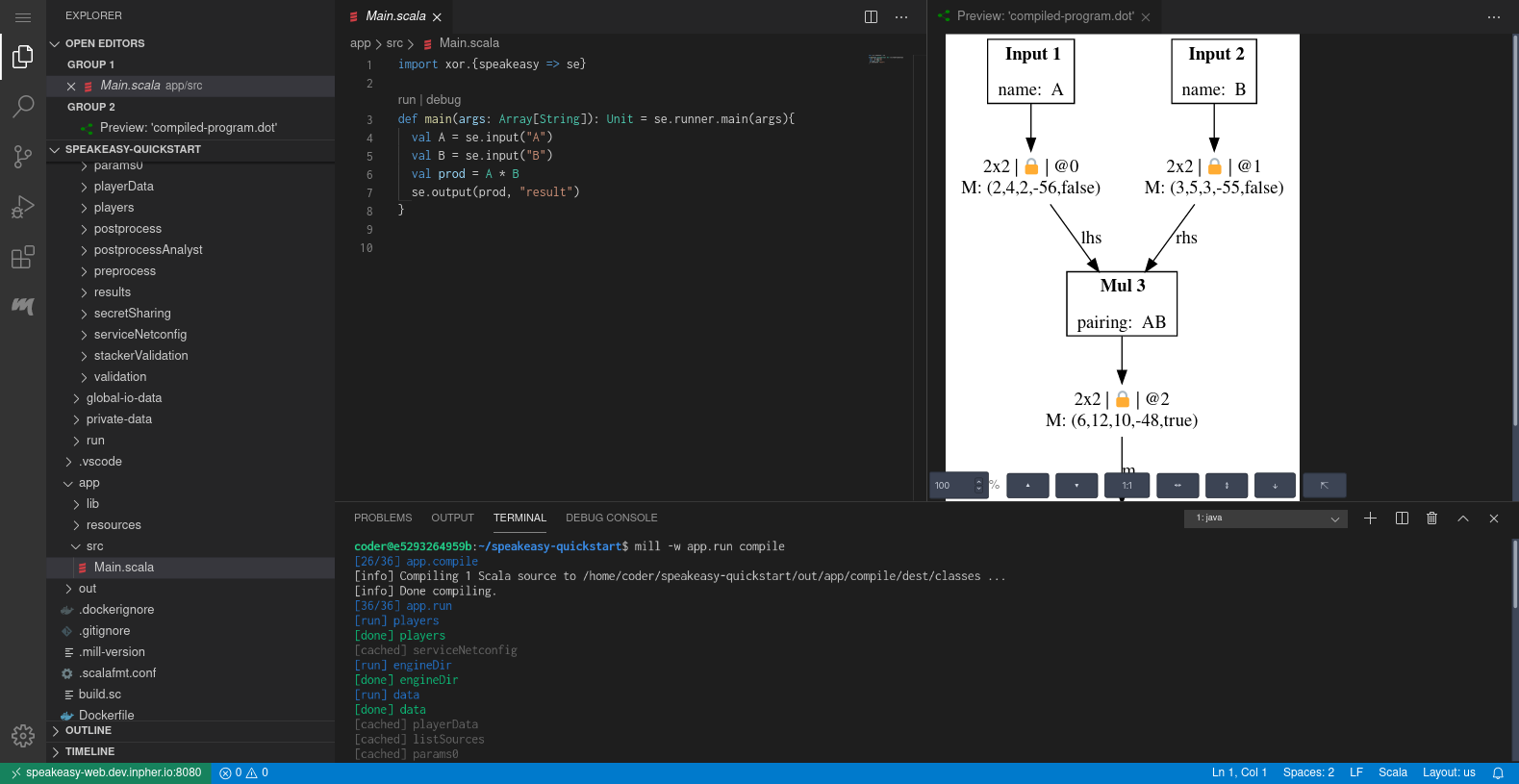
What do we mean by privacy-preserving graphs? Consider the following simple code excerpt loading two matrices via input descriptors from (possibly distinct and private) data sources, multiplying them and outputting the result via an output descriptor:

val m: Matrix = xor.input("M")
val n: Matrix = xor.input("N")
xor.output(m * n, "res")

Intuitively, one would expect that executing this code will perform the matrix multiplication. At least, this is how various classical matrix multiplication libraries in various languages (ex. numpy) would run such a program.

In XOR DSL, the execution of the above code will instead construct a graph that represents this computation. This graph can be described as follows:

The nodes correspond to builtins, that is, basic functions (or building blocks) that can be run on various privacy-preserving backends. The edges of the above graph represent how outputs of some builtins flow into inputs of other builtins, the arrows indicating the direction of the flow. The above diagram provides an intuitive and simplified graph representation of the program. In reality, the privacy-preserving graph implementation is slightly more complex.

What are the implications from a programmer's perspective? ​

In terms of day-to-day programming, it does not change much. You can still (mostly) write code as if you were planning to have it perform the computations when it is executed. This really means you can use all the features in Scala that you were used to (or that you would like to discover), as long as you respect the API.

Why are graphs of privacy-preserving programs useful? ​

The main reason is that privacy-preserving computations are executed on backends based on compute models and techniques that are very different from a traditional plaintext computation. In many cases, this requires static analyses and optimizations specifically adapted to these models. For example, the XOR Secret Computing© Platform ("XOR Platform") based on the Manticore framework represents real numbers differently than the usual floating point numbers (Double). This representation requires static analysis of the entire program to deduce certain parameters associated to the intermediate variables that ensure security and numerical precision of the computation. Designing such a tool is complex and often requires backtracking, making the graph a very convenient representation.

The graph of a privacy-preserving program is used to verify some properties such as matrix dimensions, visibilities as well as revealed intermediate variables. It can be used for various optimizations and security validations. Best of all, it enables code generation for different privacy-preserving backends (local computations on private data, MPC and FL among others).

The technique of using graphs of privacy-preserving programs described above is fairly general and appears in other frameworks as well:

• Spark constructs an execution graph of a distributed computation and sends it to clusters.
• Mill constructs a task graph for a build systems in order to establish dependencies, priorities, and caching.
• TensorFlow constructs an execution graph for a machine learning algorithm before shipping it to a cluster.
• CrypTFlow constructs an execution graph for a privacy-preserving program and executes it on an MPC backend.

Basic Examples ​

Below are three basic examples that we provide with short explanations.

Private distributed datasets (PDDs) and basic chaining of operations for FL with MPC secure aggregation ​

The code excerpts below illustrate the important concept of Private Distributed Datasets (PDDs). A PDD represents data that may be distributed across multiple partitions. Each partition of a PDD is owned by one party in a privacy-preserving computation, and together they make up one logical dataset. These are the core data structures used to create the graph of a privacy-preserving program. This is reminiscent to Spark's transformation model based on Resilient Distributed Datasets (RDDs) but adapted to the context of privacy-preserving programs.

// 1. Local model training on all clients 
val localModels: Seq[se.SecretPdd[MnistModel]] = for (client <- clients) yield {
  localTrainPy(client["model"], client["local_train_data"], learningRate = learningRate, iterNum = i)
}
// 2. Secure aggregation via XOR MPC
val aggModel: PublicPdd[MnistModel] = se.multiparty(localModels) { 
  se.mpc.mean(localModels).reveal()
}
// 3. Force evaluating the graph that computes the aggregated model update 
val resModel = se.eval(aggModel)
println(s"Current aggregated model: $resModel")

// 4. Broadcast aggregated models to clients 
clients.map{ client => client.source(resModel) }

def localTrainPy(...) {  
  println("training locally, via python calls to Tensorflow or PyTorch")
  val localModel = new MnistModel(
    se.util.execPythonTensorScript(
        "local_train.py",
        inputs = model.weights :: model.biases :: Nil,
        numOutputs = 2,
        "--data", dataFile,
        "--iternum", iterNum,
        "--learningrate", learningRate,
    )
  println("done with local training.")
  localModel
}

def batch_train(model_vars, learning_rate, batch):
    # initialize the tf.keras optimizer
    # TODO: could in theory use Adam or AdaGRAD optimizers
    optimizer = tf.keras.optimizers.SGD(learning_rate)
    # Perform one step of gradient descent using loss from `batch_loss`.
    with tf.GradientTape() as tape:
        loss = forward_pass(model_vars, batch)
    grads = tape.gradient(loss, model_vars)
    optimizer.apply_gradients(
        zip(tf.nest.flatten(grads), tf.nest.flatten(model_vars)))
    return model_vars

The first excerpt is extracted from a simple local model training (via basic Tensorflow) on a set of federated clients followed by secure aggregation of the local model updates via XOR MPC. The input/output PDDs in the local computation in Step 1. are combined with the ones in the simple MPC secure aggregation in Step 2 to form a graph of the privacy-preserving program, but this graph is not evaluated before the explicit call to eval. The second excerpt shows the evaluation of a local python script that based on Tensorflow (the third excerpt) within XOR DSL.

Logistic regression prediction ​

This example runs a logistic regression prediction:

package xor.mpc.app.logregPredict

import speakeasy.mpc as se
import speakeasy.mpc.lib

def main(using se.Context): Unit = {
  val X = se.input("X")
  val coeffs: se.Matrix = se.input("coeffs")
  val intercept: se.Scalar = se.input("intercept")

  val (predClasses, predProbs) = lib.logregPred(X, intercept, coeffs)

  se.output(predClasses, "predClasses")
  se.output(predProbs, "predProbs")
}

Notice the call to Inpher's internal algorithm library (used for various optimizations). This library is built in order to facilitate the programmer with various internal optimizations.

Computing covariances of matrix columns ​

The example above computes covariances of matrix columns in XOR MPC.

def colCovariance(x: se.Matrix, ddof: Int)(using se.Context): se.Matrix = {
  val xr: se.Matrix = se.recenter(x)
  val tmpXr: se.Matrix = (1.0 / math.sqrt((x.nrows - ddof).toDouble)) * xr
  // c.f. comment in colVariances
  (tmpXr.t * tmpXr)(pmsb := 2 * x.params.pmsb + ddof)
}

For optimization of numerical precision, the programmer is specifying certain parameters associated to the intermediate variables (essentially, upper bounds on these variables). Normally, the XOR Scala Compiler automatically deduces these bounds, yet, the programmer is able to override them.